엔트로피

정보를 표현하는데에 있어서 필요한 최소 평균 자원 량
어떻게 코딩(허프만 코드)을 해도 이거보다 낮게, 짧게 코딩할 수 없다.
Average Coding Length의 Lower Bound
1만나오는 주사위(균등한 확률, 주사위)는 안알려줘도 그만이기 때문에 정보량이 낮다.
유니폼 random variable이 엔트로피가 가장 크다.

정보를 어떻게 표현하는가?

0또는 1로 표현

최소 자원량

bit의 단위
확률이 1에 가까우면 bit길이를 자주 등장하는 것이기 때문에 bit길이를 짧게 표현한다.

왜 엔트로피는 $ H(X) = - \sum_{i = 1}^{n}p(x_i)logp(x_i) $ 형태인가

당연하다 = 사건의 확률이 높다 = 정보량이 낮다.
뻔하지 않은 이야기는 정보량이 크다.

정보량

놀람의 정도

X의 정보량 h(x) 는 p(x)에 대한 함수 해가 동쪽에 뜰 확률 $ p(east) = 0.999999 $, 서쪽에 뜰 확률 $ p(west) = 1 $이다. 따라서 $ h(west) > h(east) $이다.

확률 변수 X,Y

X는 East,West 두 가지
Y는 Rain, Not Rain 두가지
X,Y는 독립 정보 2개가 있을 때 우리가 얻을 수 있는 정보는 $ h(x,y) = h(x) + h(y) $ 로 표현할 수 있다.
정보 2개가 있을 때 우리가 얻을 수 있는 확률은 $ p(x,y) = p(x) * p(y) $ 이다.
따라서, $ f(p(x,y)) = f(p(x)*p(y)) = f(p(x)) + f(p(y)) $ 이며 로그의 형태로 $ h(x) = -log_2p(x) $로 표현이 가능하다.

이때 엔트로피(평균적인 정보량)은 각 정보량을 보낼 사건의 확률과 정보 수치 곱들의 합
$ p(east) * h(east) + p(west) * h(west) $ 이므로 $ H(X) = - \sum_{i = 1}^{n}p(x_i)logp(x_i) $ 형태가 나오게 된다. 이 식을 계산한 결과의 의미는 평균적으로 엔트로피 bits 수만큼의 정보량을 보낸다! 라고 할 수 있다.

KL Divergence란?

정답값의 분포도에서 상대적으로 얼만큼 다른지 수치도로 나타내는 값.
실제 정답값을 예측값과 비교함으로써 *어느정도*의 엔트로피가 더 필요한지 나타내는 수치
평균적으로 얼마나 손해(이득)을 보면서 정보를 보내고 있나 그 손해(이득)값을 계산하는것이다.
머신러닝에서 실제 확률 p를갖는 정보량이있고 내가 모델링한 확률이q 라면 pq와의 차이를 줄이는것을 얘기한다.
p로 모델링한게 항상 최소이기때문에 내가 모델링한 q의 entropy는 양수값이 나올것, 따라서 KL값은 양수이다.
즉, 모델링 오류때문에 발생한 추가 비용을 수식으로 나타내보면
$ (-\sum_{x}p(x)log_2q(x)) - (-\sum_{x}p(x)log_2q(x)) = -\sum_{x}p(x)log_2\frac{q(x)}{p(x)} $
차이가 크다 = 분포도가 다르다
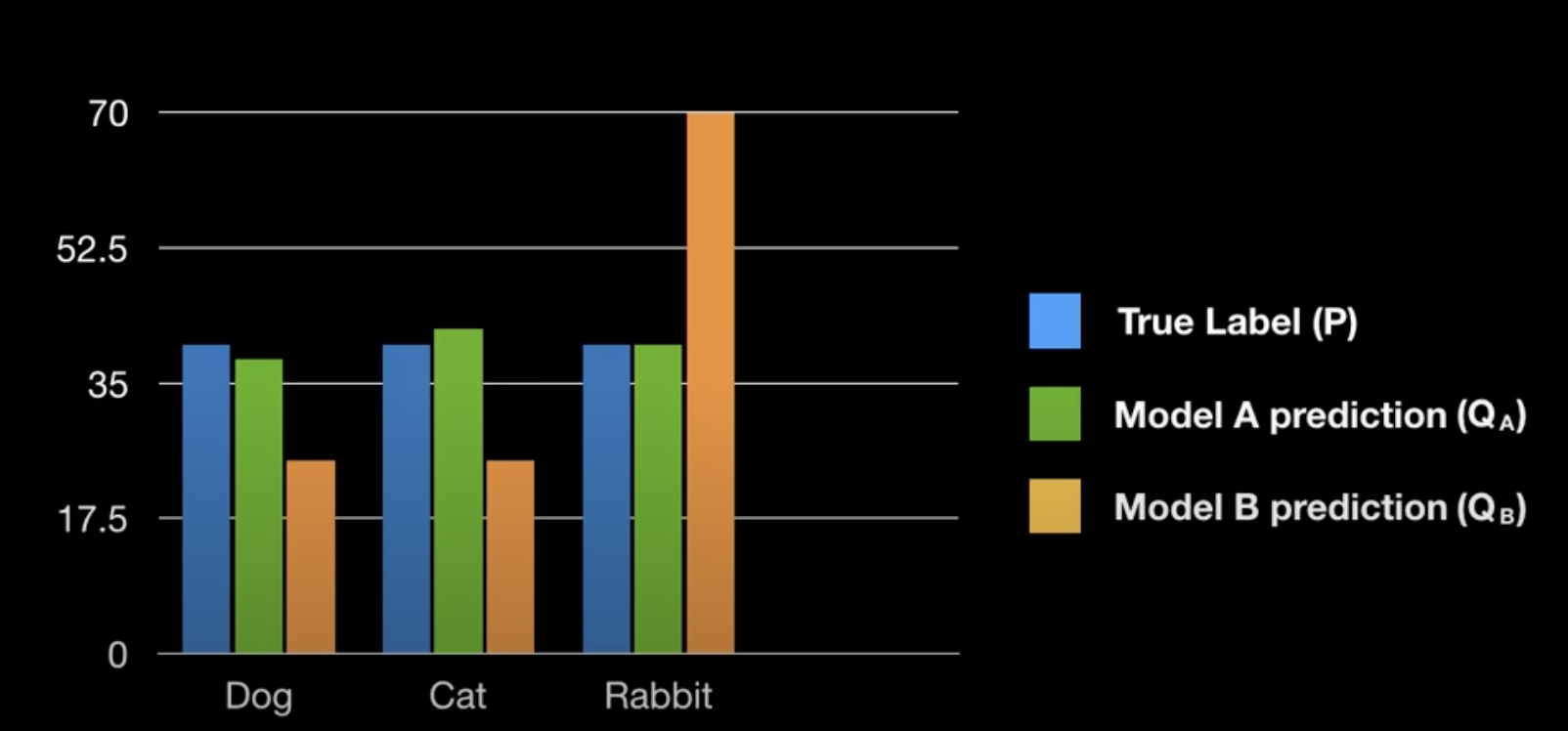
모델A가 정답과 비슷한 분포도를 가진다.
$ D_{KL}(P||Q_A) = 0.25 $
모델B는 정답과 많이 다르다.
$ D_{KL}(P||Q_B) = 1.85 $

성질

항상 양수
$ KL(p|q) > =0, (p=q 일때 0 만족) $

KL Divergence 와 Cross-Entropy의 차이

$ KL(p|q) = H(p,q) - H(p), {(이때\,H는\,정보량의\,함수)} $인것은 위에 설명한 내용들로 이해가 되었다.
이때, H(p,q)를 Cross Entropy라고 부른다. $ KL(p|q) $ 식을 q에 대해 미분하면 뒤에텀은 사라져서 최종적으로
$ H(p,q) $ 만 남기떄문에 이 식을 minimize하여 p로 가깝게 만들어나가는것이다.

Mutual Information 이란?

두사건이 독립이 아닌데 독립이라고 생각하고 모델링했을때의 수치
독립이면 0임

참고
[1] https://www.youtube.com/watch?v=Dc0PQlNQhGY&ab_channel=%ED%8C%A1%EC%9A%94%EB%9E%A9Pang-YoLab
[2] https://www.youtube.com/watch?v=7GBXCD-B6fo&ab_channel=MinsukHeo%ED%97%88%EB%AF%BC%EC%84%9D
[3] https://www.youtube.com/watch?v=z1k8HVU4Mxc&ab_channel=%ED%98%81%ED%8E%9C%ED%95%98%EC%9E%84

이 문서는 jhy156456에 의해 작성되었습니다.
마지막 수정 날짜:2023-03-22 17:00:00

[ai] kl divergence